% 平均気温が1℃高くなるってことは...
%（この記事をサイト上で見ているときはグラフが 2個表示されて文章もそのグラフに合っているはずです。このページをコピー・貼り付けして TeX で処理する場合は 4個のテキストデータファイル heikin0.tbl, heikin1.tbl, heikin0s.tbl, heikin1s.tbl が必要になります。←リンクからテキストデータをそのファイル名で、ページコピーしたファイルと同じディレクトリに保存してください。）
\documentclass[dvipdfmx]{jsarticle}
\pagestyle{myheadings}
\markright{tmt's math page}
\renewcommand\baselinestretch{1.33}
\usepackage{tikz}
\begin{document}
\section*{■平均気温が$1$\,\textcelsius 高くなるってことは$\dots$■}
西暦$2100$年には世界の平均気温が現在より$1$\,\textcelsius 高くなるとも$1.5$\,\textcelsius 高くなるとも言われている。高々$1$\,\textcelsius だ。まあ、ほんの少し温かくなるだけだから、人間の体はそれになじんでくれるだろう。しかも急に$1$\,\textcelsius 高くなるわけじゃない。$50$年以上先に$1$\,\textcelsius 高くなるだけだ。これからの世代は十分な対応ができると期待しておこう。
もちろん一年のうちには暑い日もあれば寒い日もある。まして、たとえ春の季節の中でもまた冬に戻ったかと思うような寒い日がきたり、もう夏になっちまったのかと思うような暑い日がくることもある。季節はこうして気温の高低を繰り返しながら一年をうつろう。一年の平均気温が$20$\,\textcelsius というのは、日々の気温を全部足して$365$で割った値が$20$\,\textcelsius になることを意味する。だったら平均気温が$21$\,\textcelsius になったところでたいした違いはないだろう。たまたま寒い日がちょっと少なく、暑い日がちょっと多くなればそうなるのだから。
こう考えている人がいたら、その人を極端な楽観主義者と呼ばせてもらおう。とんでもない。平均気温が$1$\,\textcelsius 高くなるってことはそんなに気楽に構えていられる事態じゃないのだ。
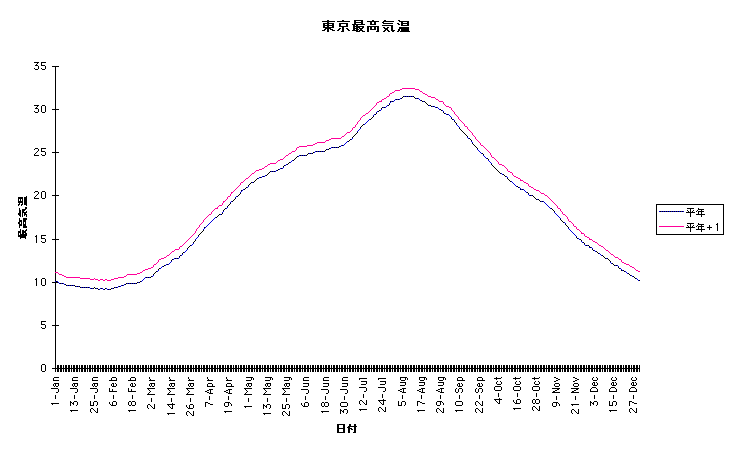
ここに用意した最初のグラフは、東京における最高気温の平年値の推移を示したグラフである。$1$月$1$日から$12$月$31$日までの毎日の平年値を線でつないである。比較のために、その平年値よりちょうど$1$\,\textcelsius 高い仮想のグラフをかき込んでおいた。これが西暦$2100$年の仮想の平均気温ということになる。
% グラフに用いたデータは$1951$年〜$1980$年の平均、すなわち$1980$年代に使われた平年値である。
% ↓TeX処理読み替え
グラフに用いたデータは$1980$年〜$2010$年の平均、すなわち$2010$年代に使われた平年値である。
% 1981--2010年の平年値を用いたグラフ（TeX処理用）
\begin{center}
\begin{tikzpicture}[x=1pt, y=3pt]
\draw (0, 35) node[below right] {\fbox{\tiny 平均気温と1度高い仮想の年間気温}} -- (0, 0) -- (366, 0);
\foreach \y in {10, 20, 30} \draw (0, \y) -- (-5, \y) node[left] {\tiny \y\,\textcelsius};
\foreach \m in {1, 2, ..., 12} \draw (30*\m-15, 0) node[below] {\tiny \m 月};
\draw[thick] plot file {heikin0.tbl};
\draw[dashed] plot file {heikin1.tbl};
\end{tikzpicture}
\end{center}
% これでは少々見にくいので、$7$月$20$日から$8$月$31$日までの推移を拡大したのが$2$番目のグラフである。下側のグラフが本来の平均気温、上側のグラフが$1$\,\textcelsius 高い仮想の平均気温である。
% ↓TeX処理読み替え
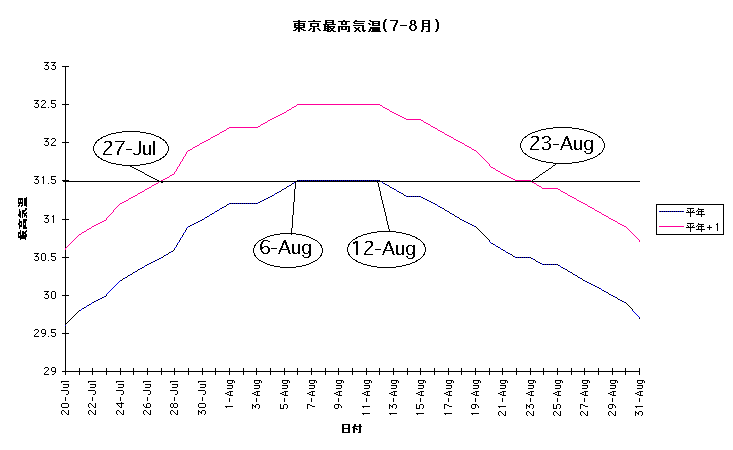
これでは少々見にくいので、$7$月$19$日から$9$月$3$日までの推移を拡大したのが$2$番目のグラフである。下側のグラフが本来の平均気温、上側のグラフが$1$\,\textcelsius 高い仮想の平均気温である。
% 1981--2010年の平年値を用いたグラフ（TeX処理用）
\begin{center}
\begin{tikzpicture}[x=5pt, y=30pt]
\draw (201, 33) node[below right] {\fbox{\tiny 平均気温と1度高い仮想の7〜8月の気温}} -- (201, 29) -- (247, 29);
\foreach \y in {29.5, 30, ..., 32} \draw (201, \y) -- (200.5, \y) node[left] {\tiny \y\,\textcelsius};
\draw[thick] plot file {heikin0s.tbl};
\draw[dashed] plot file {heikin1s.tbl};
\draw (201, 31.1) -- (247, 31.1);
\draw[dashed] (215, 31.1) -- (215, 29) node[below] {\tiny8/2};
\draw[dashed] (222, 31.1) -- (222, 29) node[below] {\tiny8/9};
\draw[dashed] (205, 31.1) -- (205, 29) node[below] {\tiny(7/23)};
\draw[dashed] (243, 31.1) -- (243, 29) node[below] {\tiny(8/30)};
\end{tikzpicture}
\end{center}
% 本来の平均気温を見てほしい。このグラフから一年の最高気温は、$8$月$6$日から$8$月$12$日にかけての$7$日間で$31.5$\,\textcelsius を記録していることが見てとれる。つまりこの$7$日間の暑さを越えれば、徐々に涼しい過ごしやすい日がやってくることだろう。
% ↓TeX処理読み替え
本来の平均気温を見てほしい。このグラフから一年の最高気温は、$8$月$2$日から$8$月$9$日にかけての$8$日間で$31.1$\,\textcelsius を記録していることが見てとれる。つまりこの$8$日間の暑さを越えれば、徐々に涼しい過ごしやすい日がやってくることだろう。
% ところで$1$\,\textcelsius 高い仮想の平均気温を見てほしい。もし未来の平均気温が現在より$1$\,\textcelsius 高いところで推移するなら、現在の暑さのピークは$7$月$27$日から始まることになる。そしてこの暑さが$8$月$23$日まで続く。この間$28$日である。
% ↓TeX処理読み替え
ところで$1$\,\textcelsius 高い仮想の平均気温を見てほしい。もし未来の平均気温が現在より$1$\,\textcelsius 高いところで推移するなら、現在の暑さのピークは$7$月$23$日から始まることになる。そしてこの暑さが$8$月$30$日まで続く。この間$39$日である。
% 何ということだろう。平均気温がわずか$1$\,\textcelsius 高くなっただけで、最高の暑さが続く期間が$4$倍に増える。もし平均気温が$2$\,\textcelsius 上昇した場合には$31.5$\,\textcelsius 以上の日は$44$日におよぶ。一年の$12$\%もの日々が真夏の特に暑い日々になるのだ。
% ↓TeX処理読み替え
何ということだろう。平均気温がわずか$1$\,\textcelsius 高くなっただけで、最高の暑さが続く期間が$5$倍以上に増える。もし平均気温が$2$\,\textcelsius 上昇した場合には$31.1$\,\textcelsius 以上の日は$52$日におよぶ。一年の$14$\%もの日々が真夏の特に暑い日々になるのだ。
暑い気候が好きな人には歓迎すべきことだろうが、私には賛成できない。平均気温が高くなりすぎることは阻止しよう。なぜなら、暑い日が増えても人間の体は順応するかもしれないが、水は相変わらず$0$\,\textcelsius で氷になり$100$\,\textcelsius で水蒸気になるのだから。
\end{document}