% 0の0乗にひそむ約束ごと
\documentclass[dvipdfmx]{jsarticle}
\pagestyle{myheadings}
\markright{tmt's math page}
\def\baselinestretch{1.33}
\usepackage{tikz}
\begin{document}
\section*{◆$0$の$0$乗にひそむ約束ごと◆}
$0^0$の答はいくつになるのでしょう。
そもそも$a^b$という書き方は、同じ数を何回も掛け算する場合の表記方法です。つまり約束ごとです。$2^5$と書けば$5$個の$2$を掛けあわせることです。つまり、
\[
2^5 = 2\times2\times2\times2\times2 = 32
\]
と計算します。では$0^0$と書けば、$0$個の$0$を掛け合わせることになりますね。あれ? $0$個の$0$を掛けるってどういうことなんでしょう。$0$個掛けるって何も掛けないことだろうから、答はきっと$0$になるんじゃないでしょうか。いえいえ、$0$乗というのは計算して答をだすのではなく、どんな数でも$0$乗したら$1$になるという約束があるのだから、$0^0$は$1$です。
さて、困りました。どちらの言い分が正しいのでしょうか。それとも$0^0$には答があるのでしょうか。
こういうときは原点に戻って考えるのが一番でしょう。一体どうして$0$乗などという表現がでてきたのでしょうか。さっきも書きましたが$2^5$の答は$32$です。同様の計算で$2^3$の答は$8$になります。もしここで$2^5\div2^3$の計算をするならば、指数の意味を考えて
\[
2^5\div2^3 = \frac{2\times2\times2\times2\times2}{2\times2\times2} = 2\times2\ (= 4)
\]
とするでしょう。ここで最後に$2\times2$、すなわち$2^2$が残りますが、これはあたかも$2^5\div2^3 = 2^{5-3}$であるように計算できることを意味します。このことを利用すれば$2^{12}\div2^{7}$の計算も、わざわざ分子・分母に$2$をたくさん書かなくても計算できることになります。すなわち
\[
2^{12}\div2^{7} = 2^{12-7} = 2^5 = 32
\]
でよいわけです。
もしこのルールがどんなときでも使えるとなれば、$2^3\div2^5$の計算も
\[
2^3\div2^5 = 2^{3-5} = 2^{-2}
\]
になるはずです。でも$-2$乗ってどういうことでしょうか。本来$2^3\div2^5$の計算は
\[
2^3\div2^5 = \frac{2\times2\times2}{2\times2\times2\times2\times2} = \frac{1}{2\times2}\ \left(= \frac{1}{4}\right)
\]
ですから、正しい答は$\displaystyle \frac{1}{4}$です。ということは
\[
2^{-2} = \frac{1}{2^2}
\]
でなければなりません。このことから「指数に負の数を使う」ことは、「指数に正の数を使って逆数に変える」ことと同じです。そこで指数に負の数を使ったときは、「逆数で表す」と約束しておくのがよさそうです。
では、$2^5\div2^5$はどうなるでしょう。これまでのルールを適用すると
\[
2^5\div2^5 = 2^{5-5} = 2^0
\]
です。$2^5\div2^5$は明らかに$1$となります。それなら$0$乗の計算結果は$1$と決めるのがよいでしょう。と、ここまでが$0$乗すると$1$になることの説明です。
だったらこの約束通り$0^0 = 1$じゃないんですか、と考えるのは早計です。$2^5\div2^5$は正しくは
\[
2^5\div2^5 = \frac{32}{32} = 1
\]
と計算できます。それがさっきのルールで$2^5\div2^5 = 2^{5-5} = 2^0$とやったから$2^0 = 1$と決められたのです。
でも$0^0$は、仮に$0^5\div0^5$の計算だとしたら、正しくは
\[
0^5\div0^5 = \frac{0^5}{0^5} = \frac{0}{0}
\]
の計算をすることになるので、答はいくつでもよいことになってしまいます(「$0$で割ることは罪深い」参照)。ですから、$0^0$の計算は「禁止」するのがもっとも妥当なのでしょう。
しかし、それではすっきりしないので、$0^0$についてもう少し考えてみることにします。
$0$は$0\times1$, $0\times2$, $0\times3$, $\dots$とみることができます。すなわち$0 = 0\times1 = 0\times2 = 0\times3 = \dots$です。このことから$0^0$の右肩の${}^0$を${}^{0\times1}$, ${}^{0\times2}$, ${}^{0\times 3}$, ${}^{\dots}$に変えてもかまわないでしょう。つまり
\[
0^0 = 0^{0\times1} = 0^{0\times2} = 0^{0\times3} = \dots
\]
です。指数法則をおおらかに用いて
\[
0^0 = (0^0)^1 = (0^0)^2 = (0^0)^3 = \dots
\]
が成り立ちます。もし$0^0$に何らかの答があって、その値が$a$であるなら
\[
a = a^1 = a^2 = a^3 = \dots
\]
ということになるでしょう。$a$は何乗しても等しいのです。こんな芸当のできる数$a$は$0$か$1$しかありえません。となれば、$0^0$の答がいくつでもよいといっても、$0$か$1$と考えるのが自然でしょう。
ためしに$x^x$というものを考えてみます。$x$の値を$2$ぐらいから始めて、
\[
2,\ 1,\ 0.9,\ 0.8,\ \dots,\ 0.1,\ \dots,\ 0.01,\ \dots,\ (0)
\]
と徐々に$0$に近づけていきましょう。$x^x$の値はどう変化するでしょうか。表は$x$の値を徐々に$0$に近づけていったときの$x^x$の値をコンピュータによって計算させてみたものです。
\begin{center}
\small
\begin{tabular}{l|l|c}
$x$ & $x^x$ & 変化の割合 \\ \hline
$2$ & $4.000000000000$ & --- \\
$1$ & $1.000000000000$ & $-3.00$ \\
$0.9$ & $0.909532576083$ & $-0.90$ \\
$0.8$ & $0.836511642073$ & $-0.73$ \\
$0.7$ & $0.7790559126704$ & $-0.57$ \\
$0.6$ & $0.7360219228178$ & $-0.43$ \\
$0.5$ & $0.7071067811865$ & $-0.29$ \\
$0.4$ & $0.6931448431551$ & $-0.14$ \\
($0.3679\dots$) & ($0.6922\dots$) & \small(正負の境目) \\
$0.3$ & $0.6968453019359$ & $+0.04$ \\
$0.2$ & $0.7247796636777$ & $+0.28$ \\
$0.1$ & $0.7943282347243$ & $+0.70$ \\
$0.01$ & $0.9549925860214$ & $+1.79$ \\
$0.001$ & $0.9931160484209$ & $+4.24$ \\
$0.00001$ & $0.9998848773725$ & $+6.84$ \\
$0.000000001$ & $0.9999999792767$ & $+11.5$
\end{tabular}
\end{center}
この表はちょっと不思議な結果を示しています。というのは、$x$の値が$2$よりもっと大きいところでは$x^x$の値はとてつもなく大きな値になると想像されます。しかし、$x$の値を$0$に近づけるほど$x^x$の値が$0$に近づくわけではないようです。$x = 0.36$あたりを底に増加に転じます。これをみると$x$がごく$0$に近いときは、$x^x$は$1$に近づくようです。それなら$0^0$は$1$とするのがよいようです。
もっと詳しく$x^x$の変化を追ってみましょう。
\[
y = x^x
\]
とおいて両辺の自然対数をとり、この両辺を$x$で微分します。
\begin{eqnarray*}
\log y = \log x^x = x\log x \\
\frac{1}{y}\,\frac{dy}{dx} = \log x + x\frac{1}{x}
\end{eqnarray*}
$y = x^x$を代入して、
\[
\frac{1}{x^x}\,\frac{dy}{dx} = \log x + x\frac{1}{x}
\]
より
\[
\frac{dy}{dx} = (\log x + 1)x^x~.
\]
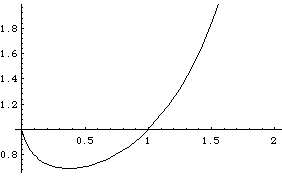
これより$x > 0$における増減表($+\infty \to 0$)を作ってみましょう。
\begin{center}
\begin{tikzpicture}
\draw[shift={(-2, 0)}] (0, 0) node {
\begin{tabular}{c|c|c|c|c}
$x$ & $0$ & $\dots$ & $\frac{1}{e}$ & $\dots$ \\ \hline
$\frac{dy}{dx}$ & $\backslash$ & $-$ & $0$ & $+$ \\ \hline
$y$ & $0^0$ & $\nwarrow$ & $(\frac{1}{e})^{\frac{1}{e}}$ & $\swarrow$
\end{tabular}
};
%
\begin{scope}[shift={(2, -1)}]
\draw[->] (-0.5, 0) -- (3.5, 0) node[right] {$x$};
\foreach \x in {1, 2, 3} \draw (\x, 0.05) -- (\x, -0.05) node[below] {$\x$};
\draw[->] (0, -0.5) -- (0, 7.5) node[above] {$y$};
\foreach \y in {1, 2, ..., 7} \draw (0.05, \y) -- (-0.05, \y) node[left] {$\y$};
\node[below left] {$O$};
\draw[domain=0.01:2.35] plot (\x, \x^\x);
\draw (0, 1) circle (1.5pt);
\draw[dashed] (0.3679, 0) node[below] {\footnotesize$\frac{1}{e}$} |- (0, 0.6922) node[left] {\footnotesize$(\frac{1}{e})^{\frac{1}{e}}$};
\end{scope}
\end{tikzpicture}
\end{center}
増減表とグラフから$x \to 0+0$のとき$x^x$の値は$0^0$に近づいていきますが\footnote{増減表は本来、左から右へ見て$\searrow$, $\nearrow$の矢印を記入しますが、$x \to 0+0$の極限を調べているので、あえて表を右から左へ見て、$\nwarrow$, $\swarrow$の矢印にしています。}、さっきの表の結果からこの値は$1$とするのがよいでしょう。もっともこれは、$0^0$を$x^x$ ($x \to 0$)の関数として見た場合の話ですから、すべての$0^0$が$1$に等しいとするものではありません\footnote{$0^0$に近づく関数は、$x^y$ ($x \to 0$, $y \to 0$)などいくらでも考えられます。}。$0^0$はやはり不定値です。
\end{document}
Mathematica による y=x^x のグラフ